Consistent Hashing Explained

By Pradyumna Chippigiri

December 26, 2025

Before we understand what Consistent Hashing is, let's understand what the problem was in traditional hashing based designs.

But firstly what is Hashing ?

Hashing

Hashing is a way to turn any input (string, number, object, file…) into a fixed-size value called a hash (or hash code) using a hash function.

Why is it useful ?

• Fast Lookup: Hash tables/maps use hashes to find items in ~O(1) average time.
• Partitioning: You can hash a key to decide which bucket/server should store it.

How do you decide if a function is a good hash function ?

• It should be deterministic meaning: Same input should generate the Same Hash (always).
• Uniform Distribution: Spreads the data evenly. (to avoid hot spots)

The Modulo %N Approach

In a distributed system, we need a way to map an incoming request (with a key like user_id) to one of our N servers.

The simplest way to do this is using the Modulo operator (%).

How it works:

We take the hash of the key: hash("user_123") = 145892.

We perform modulo N (where N is the number of servers): 145892 % 3.

The result is the index of the server (e.g., 0, 1, or 2). This is great because it’s simple, fast, and distributes keys fairly evenly across your servers. As long as N stays the same, everything works perfectly.

Example :

Say we have a user called "user_123" and we want his request to always hit a particular database. But this question may arise as to why do we even need the user to hit the same server/DB ?

Because data and cache are usually partitioned, and sending the same user to different servers causes misses, extra network calls, and higher latency. For example say:

• DB shard 0 → users 1–1M

• DB shard 1 → users 1M–2M

• DB shard 2 → users 2M–3M

If user_42’s data lives in shard 2, then: every request for user_42 must go to shard 2, sending that request to shard 0 or 1 means the data is simply not there. You can read more about sharding and its different stategies here : Sharding

So consistent routing by user key is required for correctness especially for stateful systems like Database. We may not need it for our backend services because they are stateless, and any server can handle any request. There is no requirement that the same user has to hit the same server.

But the good practise is that we send the same user to the same server even for backend services and here's why :

In-Memory Session State:

• If your server stores session data in RAM (not in Redis), you want the user to return to the same server. (Note: InMemory session states were in legacy systems, but as per modern best practises, it is always suggested to moving sessions to a distributed store like Redis)
• This is called sticky sessions. (hash by cookie/userId)

Cache Locality:

• If Server 1 already has user 42’s profile cached in memory, hitting Server 1 again is fast.

Which Parts of a system does Hashing happen ?

Hashing can happen at multiple layers like :

• Load Balancer → App Servers
• App Servers → Cache Cluster (v. common as hashing chooses which cache node stores a cachek key)
• App Servers → DB Shards (v. common as hashing chooses which particular shard a users data lies in)
• Message Queues/streaming -> Kafka partitions: partition = hash(key) % numPartitions

Commons Hashes used in the Industry

In real systems, common choices:

• MurmurHash

• xxHash

• CRC32

• sometimes SHA-1 / SHA-256 (more expensive, but stable)

For learning, you don’t need the exact function. Assume you have a black box called hash() that always gives you the same number for the same key.

The Rehashing Problem

The approach that we talked about worked great at the start Say initially we had a setup like this :

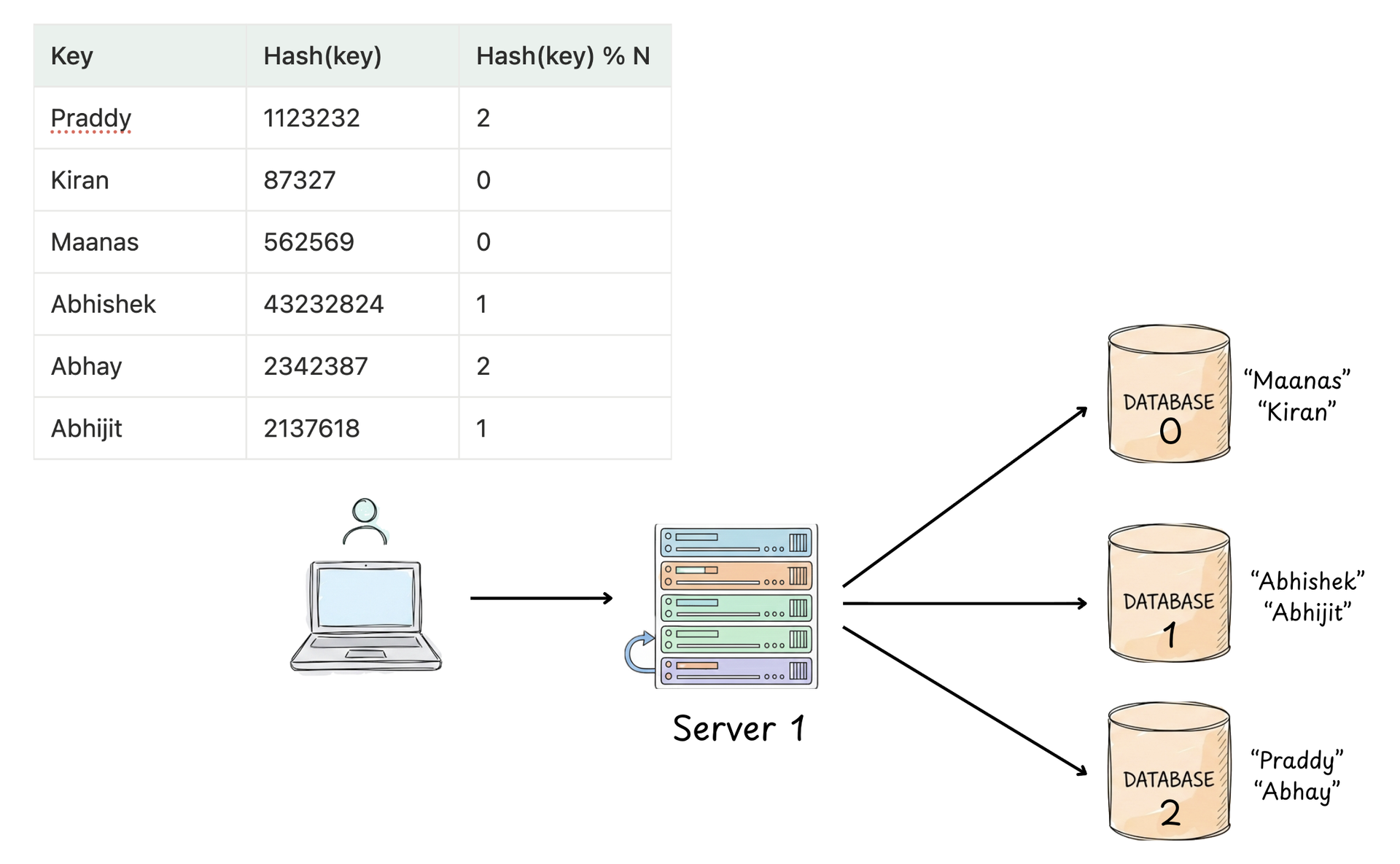
But say our site continues to grow now, so we would need to more servers, so in that case we would change the modulo in that function right, meaning if we initially had 3 servers then N was 3 and now after scaling N becomes 4. So this means, now all the data needs to be re-distributed.

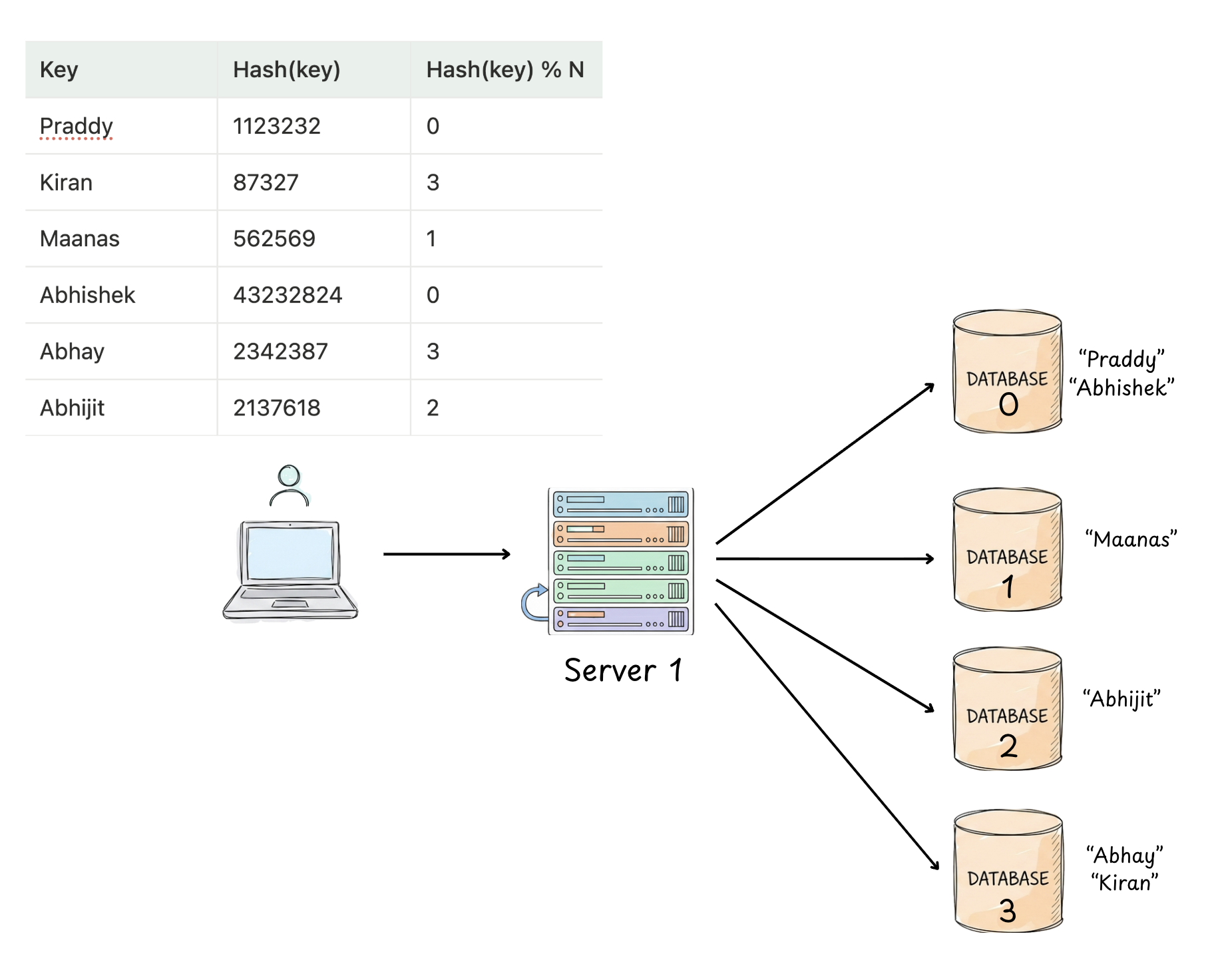
Similarly, when we want to downgrade our system, so the N = 2 now, in such cases too we would need to redestribute the data across nodes.

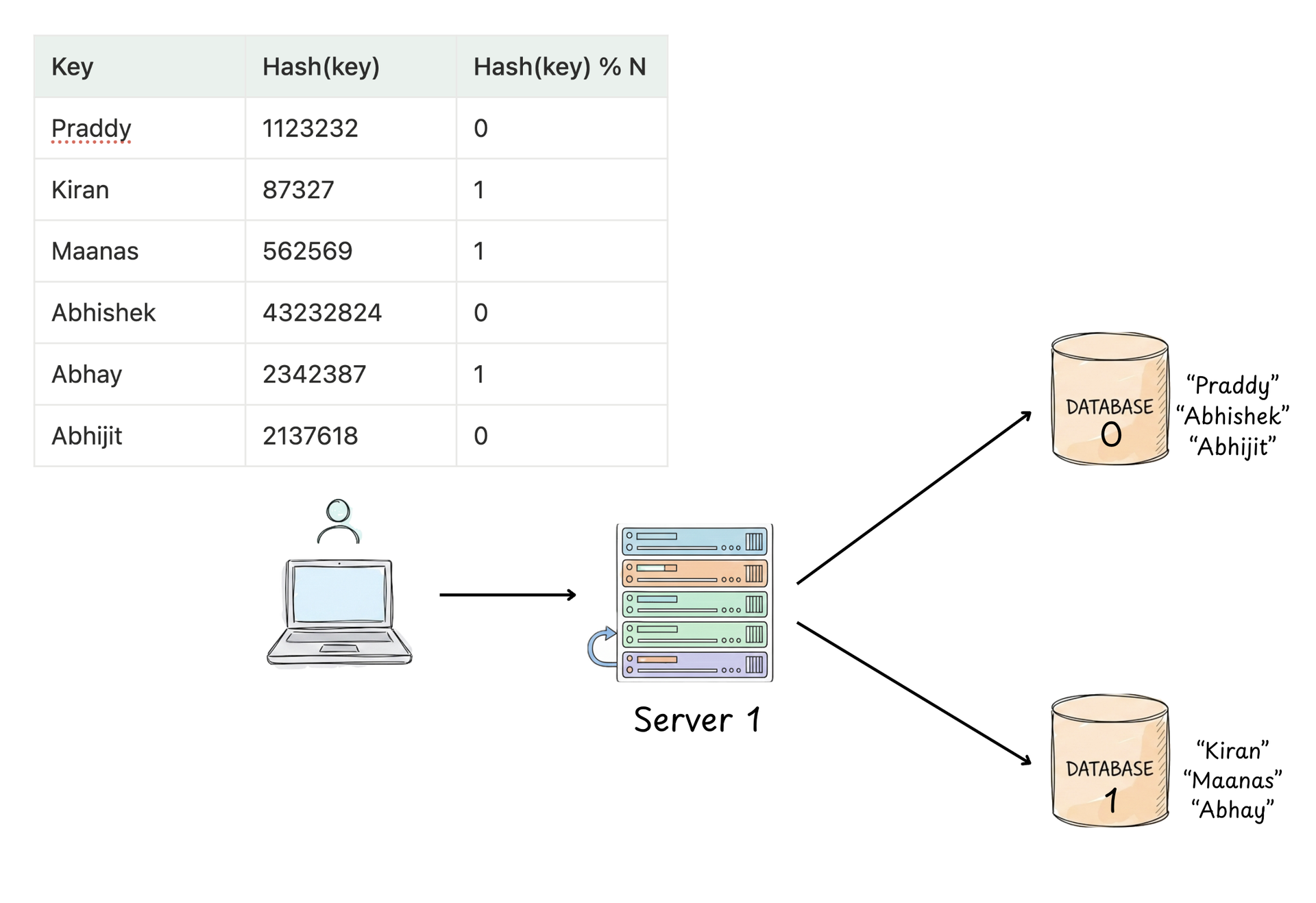
As you can observe from the above two diagrams, there is a main problem with the normal hashing which relies on the number of servers for the modulo value.

Every time there is a datastore node added/removed, we need to consider rehashing all the keys present across all of our datastore nodes. This is a super expensive operation in terms of shuffling and redestributing the whole data.

The Solution : Consistent Hashing

Consistent hashing addresses the issue that we discussed above by ensuring that only a small subset of keys need to be reassigned when nodes are added or removed.It performs really well when operated in dynamic environments, where the system scales up and down frequently

How Consistent Hashing Works ?

We imagine a ring like structure where we place our datastore nodes and the keys. And we come up with a mechanism where only a small subset of data has to be changed and in this approach we try to :

• Keep the hash function independent of the number of storage nodes

The Hash Space

We treat the output of our hash function as a fixed circular range. For example, if we use a 32-bit hash, the range goes from 0 to 2^32 - 1. Imagine this range wrapped around so that the maximum value connects back to zero .

Placing Nodes and Keys

• Nodes: We hash the node’s identifier (like its IP address or name) to get a position on the ring.
• Keys: We hash the data key to get its position on the same ring.

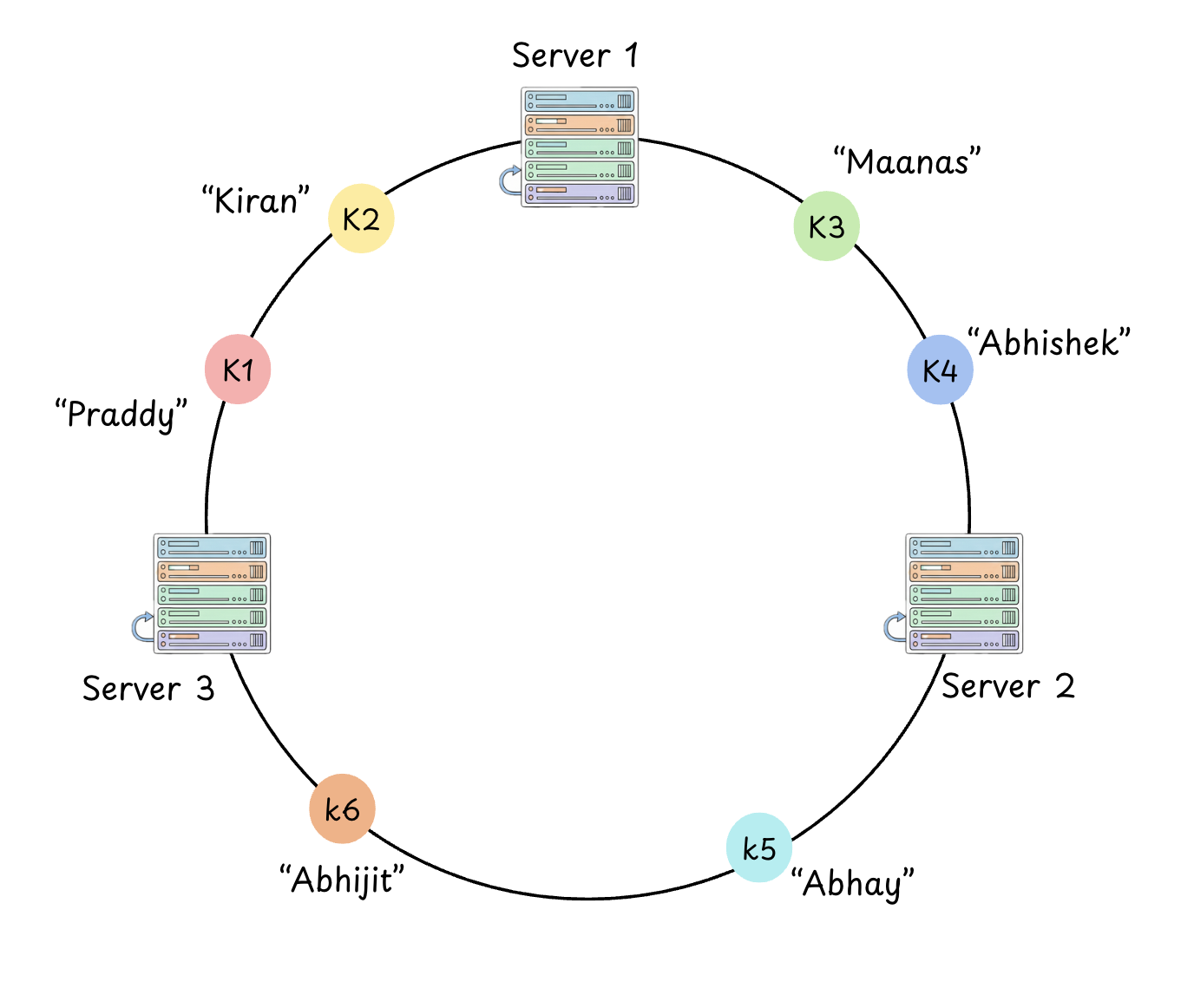
The Lookup Mechanism

To determine which node "owns" a key, we locate the key on the ring and move clockwise until we encounter the first node. That node is responsible for storing that specific piece of data.

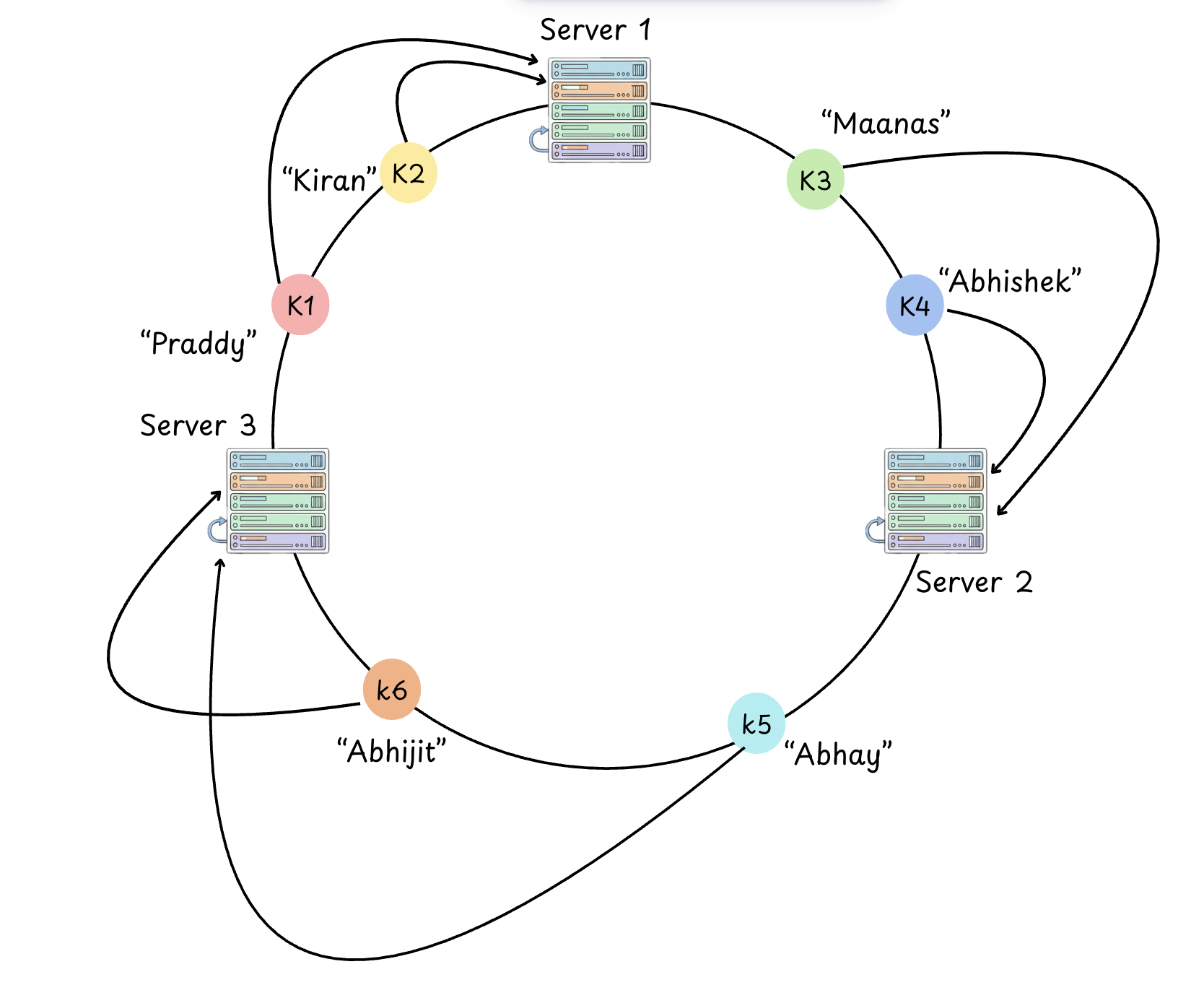
Segmenting the Ring:

When you plot M nodes on the ring, you are effectively creating M partitions. Because a good cryptographic hash function (like SHA-1 or MurmurHash) produces a uniform distribution.

• Total Hash Space: Let’s call the full range S.
• Average Segment Size: S/M
• Expected Keys per Segment: Since keys are also uniformly distributed, each segment captures roughly N/M keys.

In a traditional hash table, if a server is removed, the entire index %M breaks. In consistent hashing, the "damage" is strictly bounded.

If Server 2 fails:

• The Affected Keys: Only the keys sitting in the segment between Server 1 and Server 2 are "lost." These represent roughly N/M of your total data.
• The Re-assignment: Following the clockwise rule, these keys are now mapped to Server 3 (the next available node). System Stability: The other M-1 nodes continue to serve their own N/M keys without any interruption or data movement.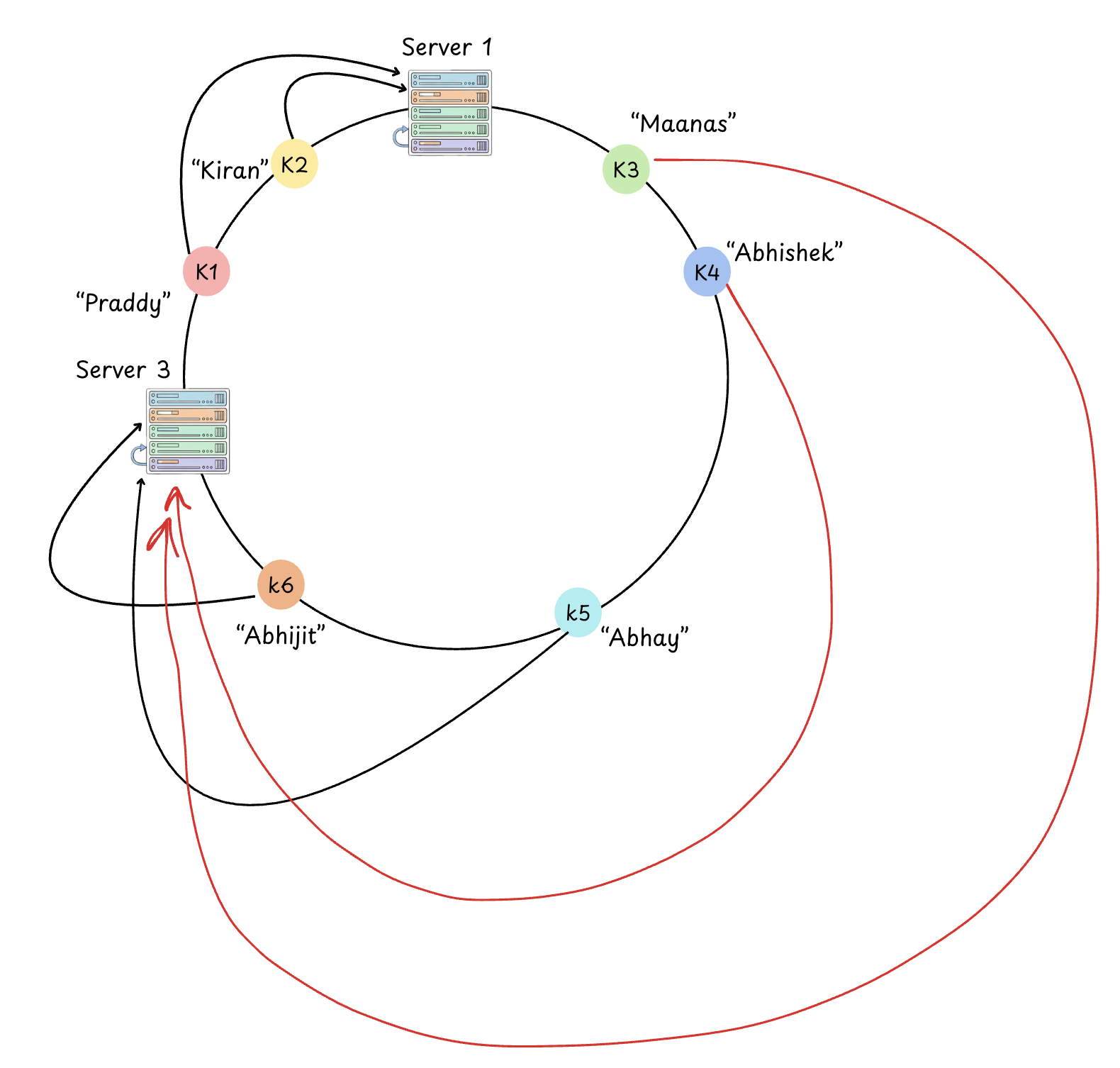

The same logic applies when adding a node. If you insert a new server node between Server 1 and Server 2. It "slices" Server Node 2's segment.
It takes over roughly N/M keys from Node 2. Other nodes are completely unaware that a change even occurred.

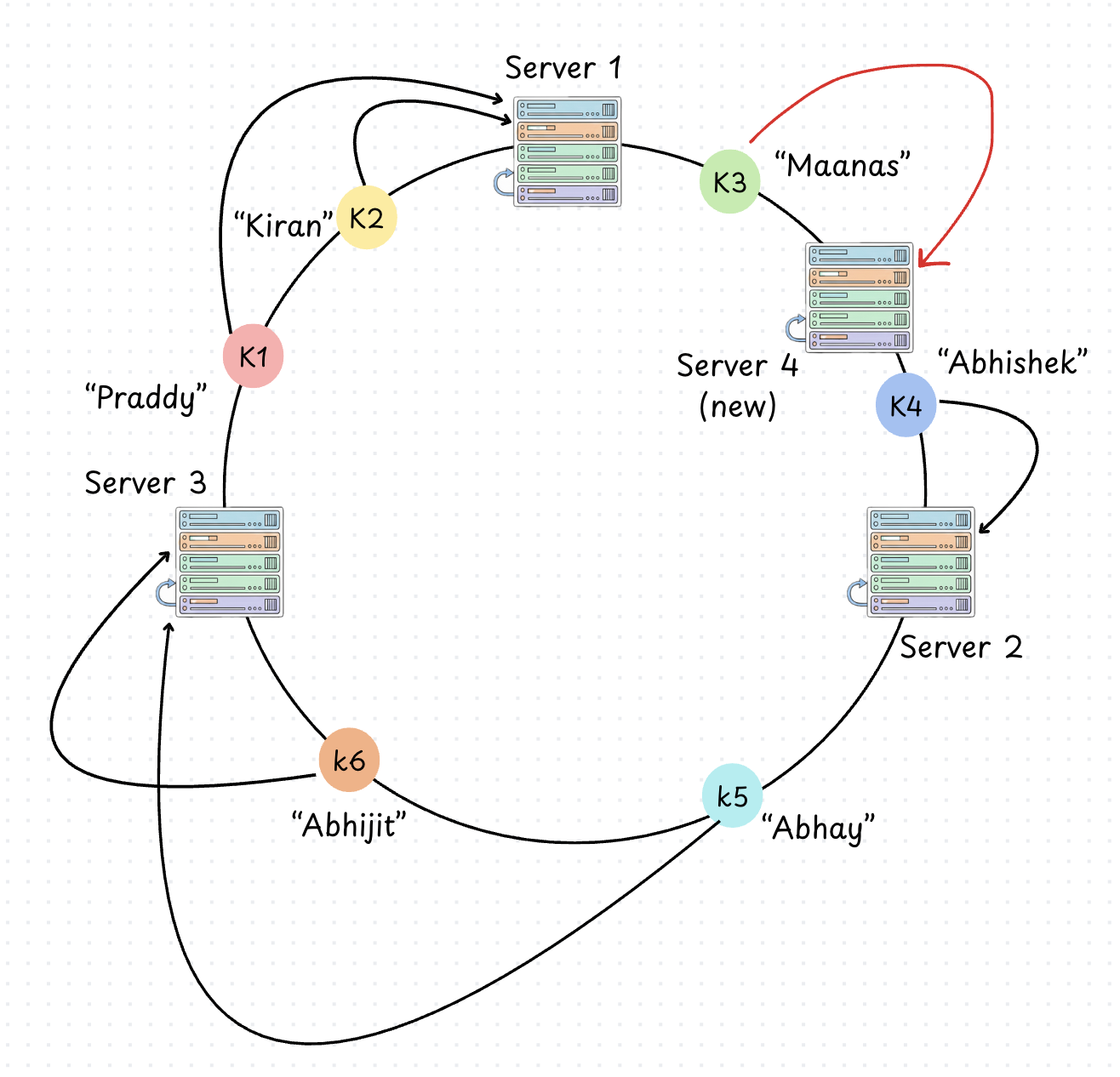
Now there is another problem, that has to be dealt with and that is the Neighbor Problem

Virtual Nodes

While it's true that only N/M keys are rehashed, there is a catch: One single neighbor (the next node clockwise) inherits the entire load of the failed node. If Node 2 fails, Node 3 now has to handle its original load plus Node 2's load (N/M + N/M).
In a high-traffic environment, this sudden 2x load on a single server can trigger a cascading failure, where Node 3 crashes from the weight, passing the combined load to Node 4, and so on. This is why Virtual Nodes are essential.

They ensure that when a physical node fails, its N/M keys are actually redistributed across multiple physical neighbors, rather than just one. Now this brings us to the topic of Virtual Copies.

Virtual nodes (VNodes) are a technique used in consistent hashing to improve load balancing and fault tolerance by distributing data more evenly across servers. Picking the image from Hello Interview

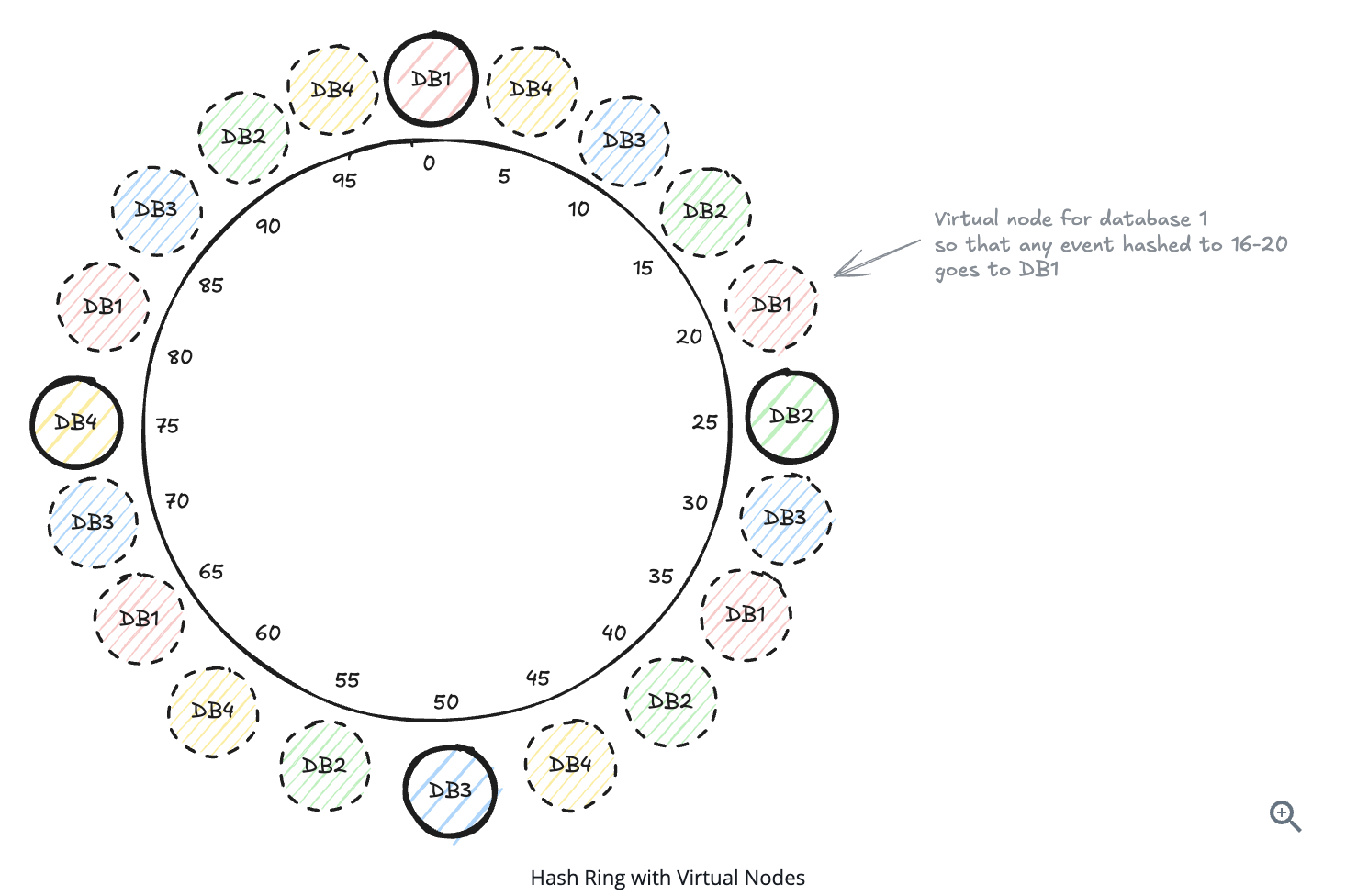
Now when Database 2 fails:

• The events that were mapped to "DB2-vn1" will be redistributed to Database 1
• The events that were mapped to "DB2-vn2" will go to Database 3
• The events that were mapped to "DB2-vn3" will go to Database 4 And so on...

Hope you liked this article, if you did then please do Subscribe to my weekly newsletter!